Povodňové režimy řek v povodí Vltavy nad nádrží Orlík


Popis metodiky pro vyhledání povodňových předpovědních analogů

Převzato z dizertační práce [Vlasák, 2008]

Zatímco aplikace metody analogu pro nepozorovaná povodí se v hydrologické praxi široce uplatnila, metoda analogu jako předpovědního nástroje pro srážko-odtokový vztah se příliš nerozvíjela. Příčinami při manuálním zpracování byly její náročná pracnost, obtíže s pojetím komplikovaných interakcí mezi uvažovanými procesy i poměrně malý počet vstupních případů pro výběr analogu, a to vše za cenu velmi hrubých výsledků. Dnes, kdy pokrok ve výpočetní technice umožňuje nové přístupy, zejména v časoprostorových analýzách zkoumaných jevů, se stává metoda předpovědního analogu znovu předmětem pozornosti. Její ambiciosnost, pokud jde o povodně, nespočívá ani tak v samostatné prognóze (kde má velkou konkurenci v podobě předpovědních modelů), jako spíš v možnostech jejího dalšího potenciálního využití pro:

Metoda předpovědního analogu se z principu vždy musí opírat o dostatečně velký soubor historických událostí. Navržená databanka povodní na Otavě je proto vhodným podkladovým nástrojem pro její testování. Metoda předpovědního analogu byla v této práci testována z hlediska její možnosti odhadnout vývoj odtokové situace na základě naměřených nebo předpovězených úhrnů příčinných srážek, nasycenosti povodí a podle sezóny výskytu.

Metoda analogu jako předpovědní nástroj

Metodu předpovědního analogu je výhodné používat tam, kde je obtížné matematicky popsat procesy vedoucí k výskytu sledovaného jevu, a kde jsou známé a zjistitelné příčiny toho jevu. Použití této metody je možné při platnosti dvou základních podmínek:


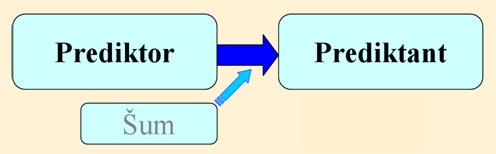
Obr. č. 1 Použité termíny při aplikaci metody předpovědního analogu

Princip aplikace metody jako předpovědního nástroje spočívá v nalezení analogické situace z hlediska příčin a předpokládá se, že stejné budou i následky. Je zřejmé, že u přírodních procesů, které jsou velmi složité a komplexní, není možné najít absolutně identický analog, a proto se hledá analog nikoliv na základě shody, ale podobnosti. Kvantifikace podobnosti mezi prediktory a stanovení jejich limit, je hlavním předmětem různých metodických přístupů a diskuzí pro aplikaci této metody.

Z uvedeného vyplývá, že metoda předpovědního analogu se uplatňuje především v těch případech, kdy nelze přírodní procesy uspokojivě modelovat a nebo kdy nejistota výstupů ze současných modelů je příliš velká. U hydrologických srážko-odtokových modelů analýzy úspěšnosti předpovědí prokázaly, že na celkové nejistotě hydrologické předpovědi se větší měrou podílejí kvantitativní předpovědi srážek z numerických meteorologických modelů než samotné srážko-odtokové modelování [Daňhelka, 2005]. Úspěšnost hydrologických předpovědí u povodňových epizod má ale k dokonalosti stále daleko, a to i při nahrazení předpovídaných srážek naměřenými, kdy se hodnotí pouze schopnost hydrologického modelu povodeň simulovat.

Přestože není obvyklé, aby byla metoda předpovědního analogu aplikovaná namísto srážko-odtokový vztahů, je možné uvést několik důvodů, proč i v dnešní době představuje tento přístup potenciální možnost pro využití v hydrologické prognóze:

Ačkoliv je zřejmé, že metoda analogu není rovnocenným předpovědním nástrojem k fyzikálním modelům, může být jejich vhodným doplněním a muže přispět k odhalení chybných modelových výstupů, které za běžných okolností jsou obtížně identifikovatelné.

Náročnost aplikace metody analogu spočívá především v nutnosti shromáždění a zpracování velkého množství dat a v úpravě ukazatelů příčin (prediktorů) do formy, která umožňuje jejich matematické zpracování, což v případě vícerozměrných veličin (prostorová data měnící se v čase – např. tlakové pole, úhrnů srážek atd.) je komplikované. Pokud se použije více různých prediktorů, pak se algoritmus výběru analogu musí optimalizovat, protože obvykle není známé numerické vyjádření funkční závislosti mezi prediktory a predikanty.

Metoda předpovědního analogu pro odhad vývoje odtokové situace byla v této práci navržena tak, aby všechny vstupy byly snadno dostupné bez využití výstupů z jiných srážko-odtokových modelů a aby nástroje použité pro kalibraci metody a výběr předpovědního analogu byly aplikovatelné v provozu hydrologického předpovědního pracoviště.

Použitá data

K tomu aby bylo možné využít co nejdelší záznam o hydrologických a meteorologických procesech, bylo nutné volit data s denním krokem, u nichž délka disponibilních řad je nepoměrně větší než u hodinových dat. Použití dat s denním krokem neumožňuje však analyzovat mezi příčinami povodní ty procesy, jejichž délka trvání je kratší. Je to především intenzita srážek a jejich podrobnější časoprostorová distribuce. Vlivy těchto faktorů na vznik povodní jsou nepochybně významné, přesto však existují okolnosti, proč absence tak důležitých informací nemusí být závažnou překážkou pro vyhledání povodní s dostatečně podobnými příčinami. V našem případě byly až na dvě výjimky (povodně 19700521, 19630701 ) všechny uvažované povodně na Otavě v Písku s průtokovou kulminací nad 145 m3.s-1 způsobené plošně rozsáhlými srážkami, u nichž většinou intenzita nedosahuje extrémních hodnot jako při lokálních bouřkových přívalech. Navíc zahrnutí vlivu sezóny do procesu výběru povodňových analogů omezuje možné rozdíly v intenzitách deště, protože vysokých intenzit je dosahováno především v letních měsících, kdy je vyšší podíl konvektivních srážek. Pohyb srážek při povodních podléhá také určitému mechanismu Jeho indikátorem může být rozložení srážek, které je v povodí Otavy silně podmíněno směrem a rychlostí proudění vzduchu. Lze tedy předpokládat, že povodňovým situacím s podobným rozložením průměrných denních úhrnů srážek předcházelo podobné proudění vzduchu a tedy i pohyb srážek.

Jediným údajem pocházejícím z hodinových záznamů byly povodňové kulminace Otavy v Písku, které byly použity pro kalibraci navržené metody pro vyhledávání analogů. Testování této metody bylo provedeno pouze na povodí Otavy po Písek, se kterým se pracovalo jako s black-box modelem, tedy bez analýzy distribuce odtoku uvnitř povodí.

Metoda byla navržena jedině pro odhad vývoje odtoku způsobeného dešťovými srážkami, padajícími do povodí za stavu, kdy vliv sněhové pokrývky není významný. V případě Otavy to není tak zásadní omezení, protože jak prokázaly předchozí analýzy povodňového mechanismu, tak u většiny povodní na Otavě v Písku byl vliv tání sněhu zanedbatelný nebo žádný. Omezení jen na dešťové povodně zmenšuje soubor možných prediktorů a usnadňuje návrh vyhledávacího algoritmu. K tomu bylo však nutné v historických řadách vyřadit ty dny, které podmínku žádného nebo malého vlivu sněhu nesplňovaly. Ze toho důvodu nebyly do procesu kalibrace ani testování metody zahrnuty některé povodně z Katalogu povodňových případů s výrazným vlivem tání sněhu na jejich vznik.

Kritériem pro identifikaci dní, kdy srážky vypadávaly ve formě sněhu, byla zvolena průměrná denní teplota vzduchu na Churáňově, který reprezentuje svojí nadmořskou výškou (1118 m n.m.) nejvyšší partie povodí. Dny, ve kterých tato teplota byla nižší než 0°C, nebyly do testování metody zahrnuty. Toto kritérium sice umožňuje, že částečně mohlo jít o srážky sněhové, ale tyto v naprosté většině padaly spíše ve formě deště. Takto jednoduchý ukazatel byl použit s ohledem na případné operativní použití metody, kde není možné počítat například s údaji o novém sněhu z dobrovolnických stanic sítě ČHMÚ, které by byly jistě vhodnějším indikátorem výskytu sněžení. Dále byly vyřazeny dny, kdy v povodí leželo větší množství sněhu. Přesahovala-li průměrná výšky vodní hodnoty sněhu na celé povodí Otavy 5 mm, nebyl tento den uvažován pro testování metody. Denní údaje o vodní hodnotě sněhu byly převzaty z výstupů z modelu SNOW – 17 [Anderson, 1973].

Pro porovnání příčin povodní byly zpracovány čtyři typy dat:

Rozsah datových řad zahrnutých do testování metody byl omezen 1. lednem 1961, od kterého jsou v klimatické databázi uloženy denní úhrny srážek ze všech stanic ČHMÚ a 31. prosincem 2006. Aby bylo možné zahrnout také velké povodně z let 1890 – 1961, byly pro tyto účely digitalizovány v dostatečném rozsahu záznamy denních úhrnů srážek ze starých srážkoměrných ročenek v době výskytu těchto povodní.

Úprava vstupních dat

Datové řady v neupravené formě v sobě nesou všechny dostupné informace o příčinách povodní. Proto by teoreticky nebylo nutné tata vstupní data dále zpracovávat a hledala by se podobnost přímo mezi nimi. Algoritmus pro nalezení podobných situací by však při množství a variabilitě těchto dat musel být velmi komplikovaný a na jeho kalibraci (trénování) by bylo potřeba mnohem více povodňových případů. Proto byla vstupní data zpracována do souhrnných charakteristik, které zároveň popisující tři základní stavy ovlivňující vznik povodně (obr. 2.) :


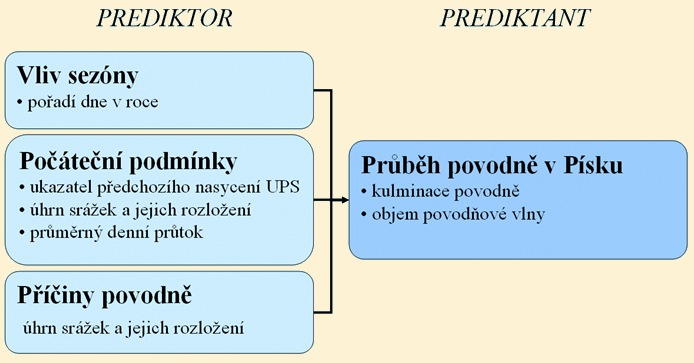
Obr. č. 2 Základní schéma použitých prediktorů a predikantů

Při vyhledávání povodňového analogu se porovnávají podobnosti prediktorů, jejichž výskyt může mít různý časový předstih před výskytem prediktantu, v našem případě průtokové kulminace povodně. V povodí Otavy se příčinné srážky mohou vyskytovat tři nebo také jeden den před kulminací. Z těchto důvodů bylo potřeba použít jiné indexované označení dnů než jako u analyzování příčin povodní, kde je klíčovým dnem den kulminace (DD).

Zde je rozhodující den, pro který je vyhledáván předpovědní analog – tedy předpovědní den. Vybraná zkratka pro tento den je PD a analogicky jako u DD jsou PD-1, PD-2 atd. dny před předpovědním dnem PD a PD+1, DP+2 atd. dny po něm. U předpovědních analogů pro povodňové situace v povodí Otavy bude předpovědní den PD většinou 1 až 3 dny před dnem kulminace DD.

Definování vlivu sezón

Působení sezóny je vyjádřeno pořadím dne PD v roce. Cílem zařazení toho ukazatele je podchytit především vliv evapotranspirace a vegetačního pokryvu. Je zřejmé, že v době mimo vegetační sezónu bude ke vzniku povodňového průtoku stačit menší množství srážek a také hodnota indexu nasycenosti UPS, který nezohledňuje změnu evapotranspirace, bude v jiném kontextu s reálnou nasyceností než ve vegetační sezóně.

Definování počátečních podmínek

Počáteční podmínky stavu nasycenosti povodí byly zpracovány do několika různých ukazatelů, založených na bilancování srážek spadlých na povodí a dále na velikosti průtoku Otavy v Písku. Pro vyjádření nasycenosti pomocí spadlých srážek byl použit ukazatel předchozích srážek (UPS). Protože index UPS počítaný pouze z údajů ze srážek nezohledňuje vliv akumulace a tání sněhu, byly vstupy denních úhrnů srážek (viz rovnice 4.1) nahrazeny součtem úhrnu pouze kapalných srážek a výšky vody z tání sněhu. Z období mezi 1961 a 2006 byly obě hodnoty získány pomocí sněhového modelu SNOW – 17 [Anderson,1973], u povodní před rokem 1961, které se všechny vyskytly v měsících květen až říjen, se předpokládá, že akumulace ani tání sněhu neprobíhaly. Průměrná hodnota indexu UPS na povodí Otavy byla vypočtena pro všechny dny mezi daty 1.1. 1961 – 31.12.2006 a pro nejbližší dny kolem velkých povodní mezi lety 1890 – 1961. K testování metody analogu byly použity hodnoty UPS pro dny PD a PD-2.

Průtok Otavy v Písku jako ukazatel nasycenosti povodí nebyl nijak upravován, pouze se použil denní průměr, který je dostupný z databáze ČHMÚ. Tento prediktor byl vztažen ke dním PD a PD-2.

Mezi ukazatele nasycenosti byly také zahrnuty průměrné dvoudenní úhrny srážek na povodí Otavy stanovené pro jednotlivé zóny, (viz kapitola 6.3.3) ve dnech PD-2 a PD-1. Vyčlenění těchto srážek mimo index UPS, je zdůvodněno tím, že tyto srážky se podílejí nejen na nasycenosti povodí, ale také na odtoku v předpovídaných dnech a proto je třeba zvýšit jejich váhu zařazením mezi ostatní přímé příčiny povodně.

Definování příčinných podmínek

Základním ukazatelem příčin povodní byly průměrné denní úhrny srážek na ploše povodí Otava. Pro účely podchycení vlivu rozložení srážek na vznik povodně bylo povodí rozděleno celkem na čtyři zóny, pro které se také vypočetly průměrné úhrny srážek. Zvolené zóny respektují základní morfologické členění povodí a navíc jejich rozložení koresponduje s oblastmi, pro které jsou v současné době rutinně vydávány kvantitativní předpovědi srážek numerickým meteorologickým modelem ALADIN, který provozuje ČHMÚ (obr. 3).


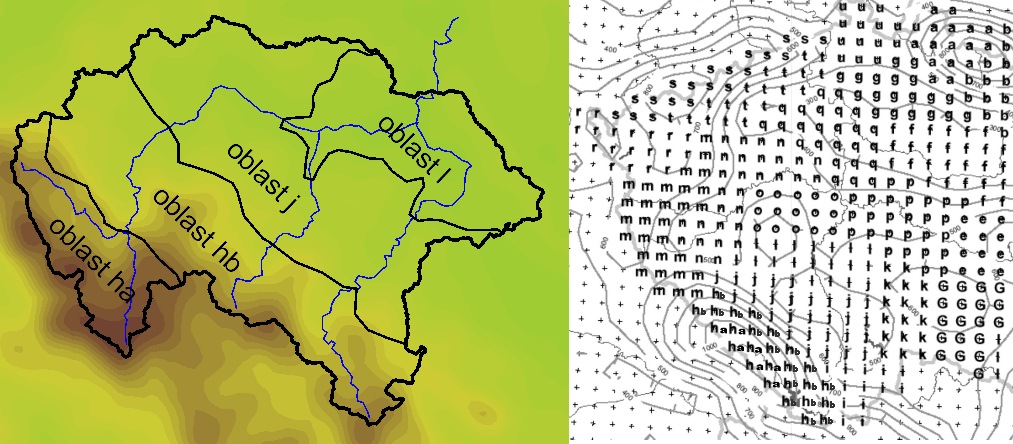
Obr 3. Oblasti povodí Otavy, pro které jsou vydávány kvantitativní předpovědi srážek modelem ALADIN ČHMÚ. Oblast h je rozdělena na podoblasti ha a h, kde jsou srážky upravovány s přihlédnutím k orografii.

Prediktor příčinných srážek byl vyjádřen jako dvoudenní průměrný úhrn ve dnech PD až PD+1 nebo třídenní úhrn PD až PD +2. V obou variantách byly vypočteny průměrné veličiny jak pro povodí Otavy po Písek tak i pro čtyři vyčleněné zóny.


Obr. č. 4 Přehled všech prediktorů použitých pro testování metody analogu

Algoritmus pro vyhledávání povodňových analogů

Cílem metody předpovědního analogu je najít v historických řadách záznam, který má dostatečně podobné charakteristiky jako nastávající situace, pro kterou je analog hledán. Pro prediktant v cílovém čase t (v našem případě je to předpovědní den PD) je tedy vyhledán v historických datech prediktant v čase u, pro který platí že prediktor F(u) se dostatečně podobá prediktoru F(t). Numericky vyjádřeno je vyhledávání analogu založeno na minimalizace rozdílu :

Min ||F(u) – F(t)|| 6.1

prohledáváním historických záznamů [Cubash, 1996]. Rovnici v této jednoduché podobě není však možné aplikovat tam, kde je použito více prediktorů popisujících různé nezávislé veličiny. Proto byl pro výběr analogu v našem případě použit postup, při kterém se porovnávají jednotlivé prediktory p (pořadí dne v roce, UPS v den PD atd.) samostatně podle vztahu

Pp = [Fp (u) – Fp (t)] 6.2

kde Pp vyjadřuje míru podobnosti hodnot u prediktoru p v čase t a u. Pokud by všechny použitě prediktory Pp byly v kauzální vztahu rovnocenné, hledal by se předpovědní analog pomocí vztahu 6.1. minimalizací součtu míry podobnosti Pp u všech prediktorů. V našem případě je však zřejmé, že vliv jednotlivých prediktorů na vznik povodně je různý (například množství srážek vyvolá povodeň spíše než pořadí dne v roce). Proto bylo nutné míru vlivu jednotlivých prediktorů vymezit zavedením váhových koeficientů.

Míru vlivu prediktoru Pp na prediktant určuje velikost koeficientu cp, jehož hodnota byla předmětem kalibrace metody. Výsledný algoritmus použitý pro vyhledávání analogu porovnává součet vážených podobnosti jednotlivých prediktorů, který je v této práci nazýván jako index podobnosti prediktorů Ipo

Ipo = 6.3

Agregace vlivů jednotlivých prediktorů do jedné hodnoty (Ipo ) umožňuje mimo jiné ohodnotit nalezené analogy podle míry podobnosti jejich prediktorů a tím odhadnout pravděpodobnost, s jakou nalezený předpovědní analog se bude blížit skutečné odtokové odezvě. Tímto postupem získává předpověď svou pravděpodobnostní hodnotu.

Podobnosti u jednolivých prediktorů

Pro zpřehlednění procesu kalibrace bylo kvantitativní vyjádření podobnosti u jednotlivých prediktorů matematicky standartizováno do podoby indexů, které se pohybují v intervalu {0,1} a kde 0 znamená nejmenší podobnost a 1 úplnou shodu. Celkem bylo pro testování metody použito 11 prediktorů, z nichž některé jsou stejné veličiny používané v jiném časovém vztahu k předpovědnímu dni PD. Výsledně bylo třeba numericky vyjádřit podobnosti u:

Pro ukazatel vlivu sezóny v roce bylo použito jednoduché kritérium
Psezona = 6.4
kde 183 je maximální možná odlehlost pořadí dnů v roce (366 dní / 2).
Podobnost úhrnů srážek, indexů UPS a denních průměrných průtoků byla standardizována podle vzorce:
PP = 6.5
kde ABS znamená absolutní hodnota a „p “ prediktor úhrn srážek (SRA), ukazatel předchozích srážek (UPS) a průměrný průtok (Qd).

Jiným postupem byla kvantifikována podobnost rozložení srážek. V tomto případě byla informace o prostorové distribuci srážek redukovány na čtyři hodnoty, které vyjadřují průměrné úhrny srážek v zónách ha, hb, j a l (obr 3.). Jako nejvhodnější způsoby vyjádření podobnosti se ukázalo porovnání relativních objemů srážek v jednotlivých zónách podle vzorce:
PRSRA = 6.6
kde Vx je objem (nikoliv průměrný úhrn) srážek spadlých na zónu x (ha, hb, j a l), V je objem srážek spadlých na celé povodí. Hodnota ukazatele P RSRA dosahuje stejně jako u ostatních prediktorů hodnot od 0 do 1 se stejným rozložením míry podobnosti.

Kalibrace metody vyhledávání předpovědního analogu

Z principů metody předpovědního analogu vyplývá, že při vzrůstající podobnosti příčin by se měly více podobat i následky jimi vyvolané. Ve skutečnosti vzájemná závislost mezi podobnostmi příčin a následků je zatížen řadou nejistot. Cílem kalibrace navrhnuté metody proto bylo identifikovat maximální míru závislosti mezi podobnostmi příčinných podmínek povodní (vyjádřených pomocí indexu podobnost preditkorů Ipo) a podobností prediktantů. Kalibrace spočívala ve zjištění optimálních koeficientů cp, které po dosazení do rovnice 6.3 davájí pro uvedené účely nejvhodnější způsob výpočtu indexu Ipo.

Podobnost nalezených analogických povodní byla hodnocena na straně predikantů (následků) podle podobnosti kulminačních průtoků a objemů průtokové vlny. Kulminační průtok byl u hledaných historických analogů zjišťován jako maximální průtok, který se vyskytl v intervalu dnů PD až PD+3. Objem povodňové vlny byl zjednodušeně stanoven jako čtyřdenní objem vody, která protekla Pískem v průběhu dnů PD až PD+3. Podobnost kulminací i objemu povodní byla numericky vyjádřena podle rovnice 6.5. Protože hodinové záznamy nutné pro určení maximálního průtoků byly v rámci disertační práce k dispozici pouze u povodní uvedených v Katalogu povodňových případů, byla metoda pro předpověď kulminačních průtoků kalibrována pouze na základě vzájemného porovnávání těchto povodní. U objemů vln, které jsou stanovené z denních průměrných průtoků byly do kalibrace zahrnuty všechny dny v období 1961-2006.

Pro kalibraci i testování metody byly použity pouze ty povodně z Katalogu, u kterých se nepodílelo na tvorbě odtoku výraznější měrou tání sněhu. Celkový počet 72 povodní byl tak zredukován na 56 případů, které jsou pro lepší názornost nazývány testovacími povodněmi.

Při zjišťování optimálních hodnot koeficientu c p se postupovalo ve dvou krocích.

Protože krok (2) byl proveden zvlášť pro predikci objemu povodně a kulminačního průtoku, byly výsledkem kalibrace dvě různé rovnice výpočtu indexu podobnosti I po . Pro předpověď kuminačního průtoku:

I po_kulminace = 0,2* Psezona (PD) + 0.2* PUPS (PD) + 0,1* PQ (PD) + 0,1* PSRA (PD-2 - PD-1) + 0,9* PSRA (PD - PD+1) + 0,1* PRSRA (PD ? PD+1) + 1* PSRA (PD - PD+2) + 0,1* PRSRA (PD - PD+2) rovnice 6.7

Pro předpověď objemu odtoku:

I po_objem = 0,1* Psezona (PD) + 0,3* PUPS (PD) + 0,3*PQ (PD-2) + 1* PQ (PD) + 0,4* PSRA (PD - PD+1) + 0,2* PRSRA (PD - PD+1) + 0.6* PSRA (PD - PD+2) + 0,2* PRSRA (PD - PD+2) rovnice 6.8

kde zkratky míry podobnosti P p jednotlivých prediktorů p znamenají:
P sezona (PD) míra podobnosti pořadí dnů PD v roce
P UPS (PD) míra podobnosti indexů UPS na povodí Otavy v den PD
P Q (PD) míra podobnosti denních průměrných průtoků Otavy v Písku v den PD
P Q (PD-2) míra podobnosti denních průměrných průtoků Otavy v Písku v den PD-2
P SRA (PD-2 - PD-1) míra podobnosti dvoudenních úhrnů srážek na povodí Otavy ve dnech PD-2 až PD-1
P SRA (PD - PD+1) míra podobnosti dvoudenních úhrnů srážek na povodí Otavy ve dnech PD až PD+1
P RSRA (PD - PD+1) míra podobnosti rozložení dvoudenních úhrnů srážek v zónách ha, hb, j a l ve dnech PD až PD+1
P SRA (PD - PD+2) míra podobnosti třídenních úhrnů srážek na povodí Otavy ve dnech PD až PD+2
P RSRA (PD - PD+2) míra podobnosti rozložení třídenních úhrnů v srážek v zónách ha, hb, j a l ve dnech PD až PD+2

U prediktorů: index UPS na povodí Otavy v den PD-2 a rozložení dvoudenních srážek v zónách ha, hb, j a l ve dnech PD-2 až PD-1, byl u obou rovnic vypočítán optimální koeficient c p rovný nule, což znamená, že tyto veličiny při uvažovaném přístupu nemají signifikantní vliv na podobnost prediktantů u nalezených předpovědních analogů, a proto nebyly pro výběr historického předpovědního analogu použity.

Hodnoty koeficientů c p v rovnicích 6.7 a 6.8 určují mimo jiné váhu, tzn. velikost vlivu podobnosti jednotlivých prediktorů na podobnost hledaných prediktantů. U předpovědi kulminačního průtoku mají nejvyšší váhy podobností dvoudenních a třídenních úhrny srážek. Vliv ostatních prediktorů je výrazně nižší. U předpovědí objemů má nejvyšší váhu podobnost průměrného denního průtoku Otavy v Písku o něco nižší pak podobnosti dvou a třídenních srážkových úhrnů.

Výsledný vztah mezi velikostí indexu I po a mírou podobnosti kulminačních průtoků respektive objemem povodní je zobrazen na obrázku 6.5. Optimalizací koeficientů c p bylo u těchto závislostí dosaženo u předpovědí kulminačních dosaženo maximálního korelační koeficientu R 2 = 0,39 a u předpovědi objemů povodní R 2 = 0,61.

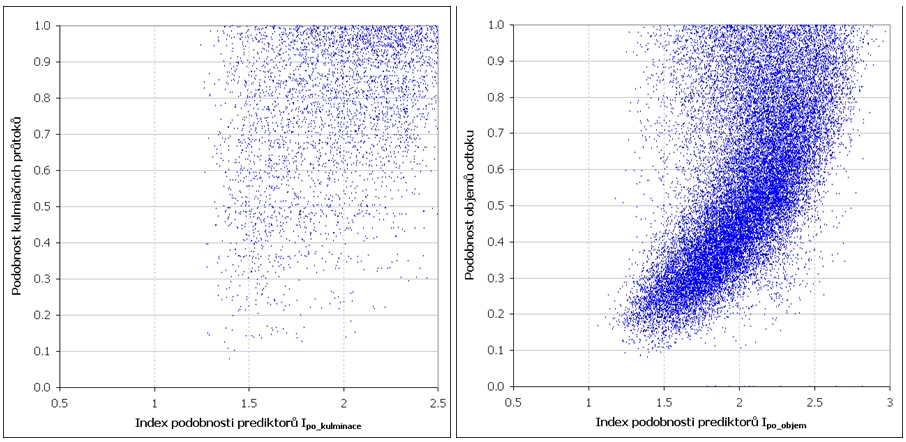
Obr. č. 5 Závislost mezi indexem podobnosti prediktorů Ipo a podobností předpovídaných charakteristik odtoku – kulminačního průtoku a objemu odtoku.

Rozptyl hodnot zobrazených na obrázku 6.5 definuje kromě funkčnosti vztahu také pravděpodobnostní hladiny, které určují s jakou pravděpodobností bude při určité hodnotě indexu Ipo překročena míra podobnosti prediktatnů. Tato informace přidává předpovědím pravděpodobnostní rozměr.

Vyhodnocení pravděpodobnostního rozměru předpovědí bylo provedeno pouze pro předpovědi objemů odtoku. Testování metody pro odhad kulminačního průtoku bylo omezeno pouze na vyhledávání předpovědního analogu mezi testovanými povodněmi (56 případů) navzájem. Jelikož většina těchto povodní vykazovala kulminaci mezi 145 m 3 .s -1 až 200 m 3 .s -1 byly by si vybrané povodně vzájemně podobné i při náhodném výběru předpovědního analogu. Průměrné míry podobnosti kulminačního průtoku by při zahrnutí odtokových situací, které svým maximálním průtokem nepřekročily hranici 1leté vody byly ve skutečnosti menší a měly jiný rozptyl.

Pro zvolené intervaly hodnot indexu Ipo byly vypočteny histogramy četností výskytu povodňových analogů s určitou velikostí míry podobnosti objemů odtoku. Z těchto histogramů byly zkonstruovány čáry překročení, které určují, s jakou pravděpodobností se bude při určité hodnotě indexu Ipo objem odtoku nalezené historické povodňové události podobat reálné situaci. Například je-li k daným charakteristikám příčin nalezena v historických řadách situace, u které při porovnání příčin je vypočtena velikost indexu podobnosti Ipo = 2,2, pak z čar překročení zobrazených na obrázku 6.6 vyplývá, že s 50 procentní pravděpodobností bude míra podobnosti objemů větší 0,8 (při předpovědi objemu odtoku například 400 mil. m 3 to znamená, že reálný objem se bude podle rovnice 6.5 nacházet v intervalu 267 – 600 mil. m 3 ).


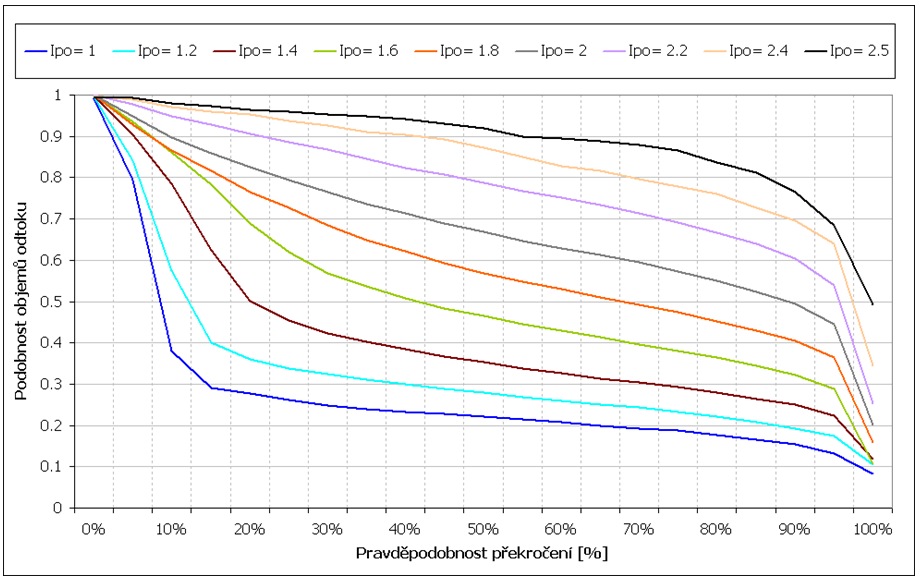
Obr. č. 6 Čáry překročení podobností objemů odtoku k nalezeným analogickým povodním při různých hodnotách indexu podobnosti objemů odtoku

Při již známém algoritmu výpočtu indexu Ipo bylo možné vyhodnotit úspěšnost navržené metody na základě porovnání nejvhodnějších předpovědí k 56 testovaným povodní. Nejvhodnější předpovědní analog ke každé testovací povodni byl v historických řadách vybrán na základě nalezení dne s nejvyšším hodnotou indexu Ipo. Z výběru byly pochopitelně vyřazeny dny v bezprostřední blízkosti testovací povodně. Graficky pak byly porovnány předpovídané kulminační průtok a objem odtoku se skutečnými. Tyto výsledky jsou zobrazeny na obrázcích 6.7 a 6.8.



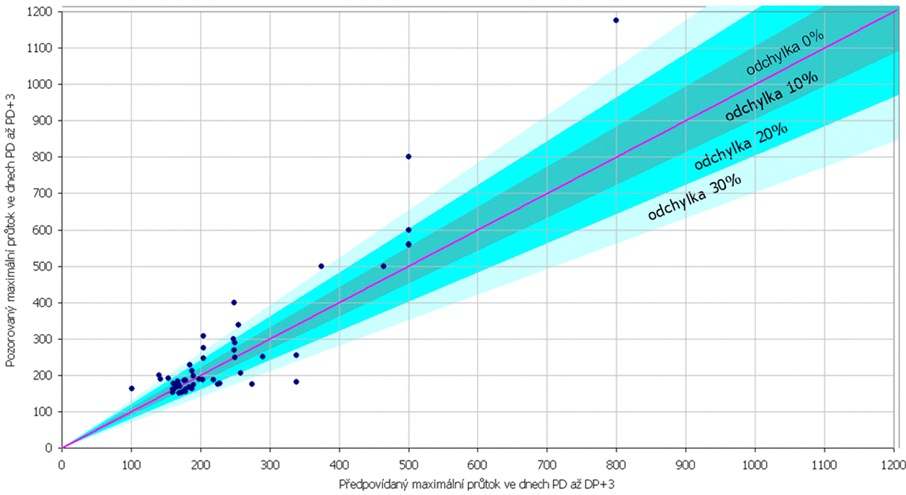
Obr. č. 7 Porovnání předpovídaných a pozorovaných maximálních průtoků u 56 povodní Otavy v Písku, jejichž charakteristiky byly použity pro testování metody předpovědního analogu



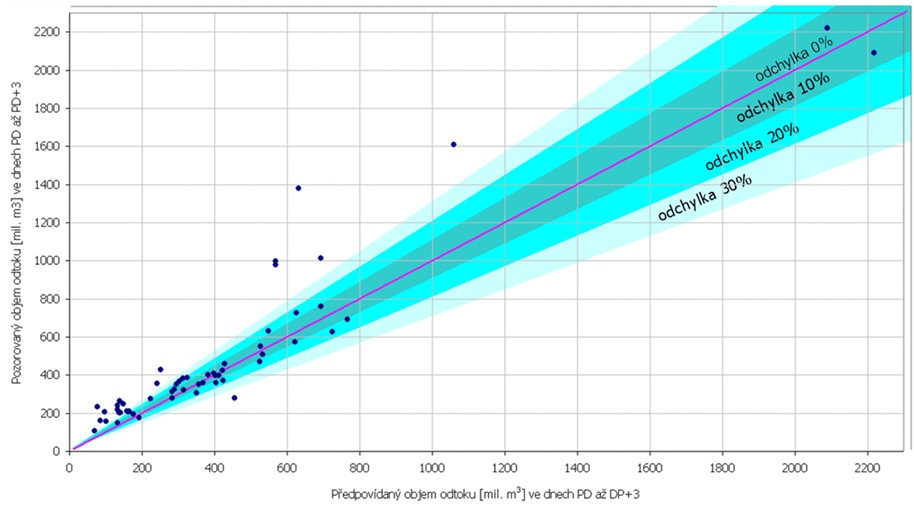
Obr. č. 8 Porovnání předpovídaných a pozorovaných objemů odtoku u 56 povodní Otavy v Písku jejichž charakteristiky byly použity pro testování metody předpovědního analogu

Výsledky navržené předpovědní metody

Navržená metoda předpovědního analogu je založená na syntéze charakteristik příčin povodně do jednoho indexu (Ipo), na jehož velikosti je závislá také míra podobnosti maximálního průtoku a objemu odtoku v následujících čtyřech dnech. Výsledky ukazují, že při porovnání uvedených charakteristik příčin povodní dosahuje vyšší závislosti na indexu Ipo podobnost předpovídaných a skutečných objemů odtoku. Pro nalezení optimálního předpovědního analogu pro odhad objemu odtoku má největší vliv podobnost mezi průtoky Otavy v Písku v předpovědní den a mezi dvoudenními a třídenními srážkovými úhrny ve dnech následujících. Statistické vyhodnocené předpovědních analogů za všechny dny období 1961 – 2006 umožňuje u každé předpovědi stanovit pravděpodobnostní interval, ve kterém by se měl nacházet předpovídaný objem.

Z porovnání nejvhodnějších předpovědních analogů (s nejvyšší hodnotou indexu Ipo k 56 testovaným povodním) vyplývá, že i navržená metoda pro předpověď kulminačním průtoků má poměrně dobré výsledky. Předpovězený kulminační průtok se u 56 testovaných povodní odchyloval od skutečnost v 16 případech o méně než 10%, u 14 předpovědí o méně než 20%, u 14 předpovědí o méně než 30% a 12 předpovědí se lišilo více jak 30%. U předpovědí objemu odtoku se u 56 testovacích povodní 15 předpovědí lišilo od skutečnosti o méně než 10%, 13 předpovědí o méně než 20% ,10 předpovědí o méně než 30% a 10 předpovědí o více jak 30%. Například objem druhé vlny povodně ze srpna 2002 povodně by se od předpovědního analogu, kterým je povodeň 18900904 lišil pouze o 8%!

Otázkou zůstává malý vliv podobnosti prostorového rozložení srážkových úhrnů na nalezení optimálního předpovědního analogu (viz rovnice 6.7 a 6.8). To je překvapivé zejména proto, že provedené analýzy povodňového mechanismu Otavy prokázaly důležitost tohoto faktoru na charakter vývoje odtokové situace. Lze se domnívat, že pokud by algoritmus výpočtu indexu Ipo mohl být kalibrován na podobnost takového procesu jako je utváření tvaru povodňové vlny, k jehož řešení nebývá vždy dostatek potřebných podkladů, pak by byl význam rozložení srážek vyšší. Proto zpřesnění této metody pro stanovení průběhu odtoku vyjádřeného tvarem průtoků vlny je otázkou pro další rozvoj toho přístupu k hydrologickým předpovědím.

Postup při aplikaci navržené metody předpovědního analogu v provozu hydrologického předpovědního pracoviště je následující: